CORFUNC

The CORFUNC program performs correlation function analysis of one-dimensional SAXS or SANS patterns, or generates a model-independent volume fraction profile from a one-dimensional SANS pattern from an adsorbed layer.

Program Development (as of July 2004)

Contact: Dr Stephen King, s.m.king@stfc.ac.uk, www.isis.stfc.ac.uk/instruments/small-angle-scattering.html, manual

 

 

Only the Java versions of the program currently perform the volume fraction profile analysis.

 

Correlation Function

The correlation function [1] [2] [3] [4] [5] [6] is the Fourier transform of the scattering curve and may be analysed in terms of an ideal lamellar morphology [7] to obtain structural parameters describing the sample. This is illustrated graphically in Figure 1 and Figure 2 below:

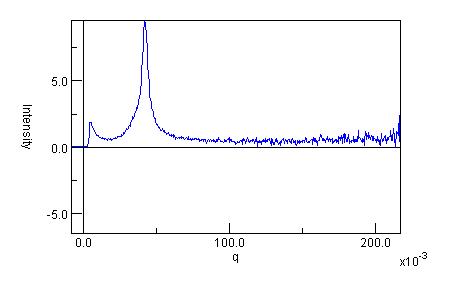
Figure 1 (upper) : One-dimensional SAXS data, (lower) : One-dimensional correlation function calculated from the SAXS data using CORFUNC.

Figure 2: Schematic representation of the one-dimensional correlation function showing the parameters that may be obtained:

Long period  = Lp
Average hard block thickness = Lc
Average core thickness = D0
Average interface thickness = Dtr
Average soft block thickness = La = Lp - Lc
Local crystallinity = φ1 = Lc / Lp
Bulk crystallinity = φ = Γmin / (Γmin + Γ*)
Polydispersity = Γmin / Γmax
Electron density contrast = (ρc - ρa)² = (Δρ)² = Q Γ*/ (φ (1 - φ))
Specific inner surface = Os = 2φ / Lc
Non-ideality = (Lp - Lp*)² / Lp ²

where Q is the Invariant.

The analysis is performed in 3 stages:

(a) Extrapolation of the experimental scattering curve to q = 0 and q = infinity,
(b) Fourier transform of the extrapolated data to give the 1-D correlation function, and
(c) Interpretation of the 1-D correlation function based on ideal lamellar morphology.

 

Volume Fraction Profile

The volume fraction profile is a distribution function that describes how the number density of an adsorbed species (typically a surfactant or polymer) varies with distance from an interface (such as a particle surface) [8] [9]. It may be analysed [10] [11] [12] to obtain parameters describing the extent (thickness) of the adsorbed layer, the amount of material adsorbed, and what proportion is "bound" at the interface. It is obtained by a Hilbert transformation of the scattering data. 

This is illustrated graphically in Figure 3 and Figure 4 below:

Figure 3 (upper) : One-dimensional SANS data, (lower) : Volume fraction profile generated from the SANS data using CORFUNC.

Figure 4: Representative volume fraction profile types showing the parameters that may be obtained:

Adsorbed amount = Γ
Bound fraction = <p>
Hydrodynamic layer thickness (or extent) =
Second moment thickness =

Possible other parameters that may be derived include:

Surface coverage =
Distance between grafting points = D

 

The analysis is performed in 3 stages:

(a) Extrapolation of the experimental scattering curve to q = 0 and q = infinity,
(b) Hilbert transform of the extrapolated data to give a segment density distribution, and
(c) Normalisation of the segment density profile to give the volume fraction profile.

 

References

Also see the original article about CORFUNC in Fibre Diffraction Review, (1994) 3, 25-29  or search STFC ePublication Archive for other FDR archive material.

• Strobl, G. R. and Schneider, M. J., Polym. Sci. (1980) 18, 1343-1359.
• Balta Calleja, F. J. and Vonk, C. G., X-ray Scattering of Synthetic Polymers, Elsevier, Amsterdam 1989, 247-257.
• Balta Calleja, F. J. and Vonk, C. G., X-ray Scattering of Synthetic Polymers, Elsevier, Amsterdam 1989, 257-261.
• Koberstein, J. and  Stein R. J., Polym. Sci. Phys. Ed. (1983) 21, 2181-2200.
• Press, W. H. et al., Numerical Recipes: the Art of Scientific Computing, Cambridge University Press 1986.
• Balta Calleja, F. J. and Vonk, C. G., X-ray Scattering of Synthetic Polymers, Elsevier, Amsterdam 1989, 261-288.
• Glatter, O. and Kratky, O., Small Angle X-ray Scattering, Academic Press Inc., London Ltd. 1982, 433-466.
• Crowley, T. L., D.Phil Thesis, University of Oxford, 1984.
• Cosgrove, T. et al., Faraday Symp. of the Chem. Soc., No.16, Royal Society of Chemistry, London 1981
• Cosgrove, T., J. Chem. Soc. Faraday Trans. (1990) 86, 1323-1332
• King, S. M. et al., Applications of Neutron Scattering to Soft Condensed Matter, Gordon & Breach, Amsterdam 2000, 77-105
• King, S. and Flannery, D., Fibre Diffraction Review (2005) 13, 19-22

Appendix

The ideal lamellar model consists of alternating crystalline and amorphous lamellae that are placed in stacks of dimensions that are large enough not to affect the small angle scattering [7]. The model is assumed to be isotropic i.e. no preferred orientation is accounted for. The correlation function of such a system varies in one direction only, perpendicular to the lamellae. The variation of the correlation function in this direction is described by the one-dimensional correlation function.