The family of compounds with the hexagonal perovskite structure exhibits magnetic properties and exotic phenomena that are an active subject of investigation. Indeed, the geometrical arrangement and electronic structure of the magnetically active ions present in these compounds make the characterisation of the magnetic ground state challenging.
The magnetic ground state of two ruthenium-based hexagonal perovskite compounds, Sr3LiRuO6 and Sr3NaRuO6, was determined thanks to a combination of characterisation measurements and diffraction techniques that captured the orientation of the magnetic spins for the ruthenium (Ru) ions. The study of the physical properties (such as heat capacity and susceptibility) of the two considered compounds showed that the majority of the magnetic moment is antiferromagnetic, with a small ferromagnetic component observed predominantly within a specific lattice plane. These results were further supported by resonant X-ray diffraction measurements of single crystals of Sr3LiRuO6 and Sr3NaRuO6 – performed on the Materials and Magnetism beamline (I16) at Diamond Light Source.
The X-ray measurements required the reconfiguration of I16 for low energies, making this the first experiment where I16 was operated in the range between 2.7 keV and 3.4 keV. Based on the collected data, a theoretical analysis indicated that antisymmetric exchange interactions control the magnetic order in the compounds through structural distortions and magnetoelastic coupling. The generality of these results might help shed light on other systems in the family of hexagonal perovskites.
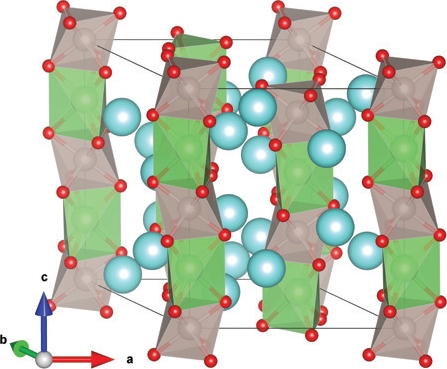
The family of compounds crystallising in the hexagonal variant of the perovskite structure, whose prototype is Sr4PtO6, exhibits a plethora of fascinating and, in several cases, unaccounted for magnetic properties1,2. The crystal structure (Fig. 1) consists of chains of face sharing trigonal prisms and slightly distorted octahedra running along the c axis of the crystal, forming a triangular lattice in the ab plane. It is easily seen that this arrangement can lead to magnetic frustration: the inability to satisfy simultaneously all the magnetic exchange interactions. Such a case occurs in presence of ferromagnetic (FM) intra- and antiferromagnetic (AFM) inter-chain magnetic interaction and a strong local anisotropy2. A different situation can occur when the local anisotropy is suppressed and the interactions are all predominantly antiferromagnetic3. In this case the system is only weakly frustrated and the magnetic structure in a first approximation can be rotated as a whole without an associated energy cost. Such a situation is rare and enhances the importance of higher order terms in selecting the magnetic ground state of the system. Sr3ARuO6, with A = (Li, Na), offers an ideal system to explore this scenario. The magnetically active ion is the Ru5+ in the octahedral configuration, hence it has an expected effective spin only moment of ~3.87 μB, however the spatial extension of the 4d electronic orbitals can suppress part of the available moment in the ordered configuration. Similar systems formerly investigated using neutron scattering exhibited a propagation vector k=(0,0,0), meaning that the periodicity of the magnetic structure is equal to that of the atomic structure, and that within the Landau theory of second order phase transitions can correspond to several magnetic moment arrangements (Fig. 2). From left to right, the first two cases are respectively FM and AFM ordering along the chains and maintain the trigonal symmetry, whereas the last two cases have the moments mostly in the basal planes, which implies a loss of the 3-fold symmetry. In both these configurations the magnetic moments are not obliged to lie in the basal plane as the symmetry of the C2/c (C2’/c’) space groups allows for an AFM (FM) component along c. Note that c’ denotes a time reversal of the magnetic symmetry along c. The same consideration applies to in plane collinearity that is not enforced by symmetry. However large deviation from collinearity or large FM components along c would result in a large FM component on top of the nuclear reflections, not observed by neutron diffraction and unjustified in systems dominated by symmetric exchange.
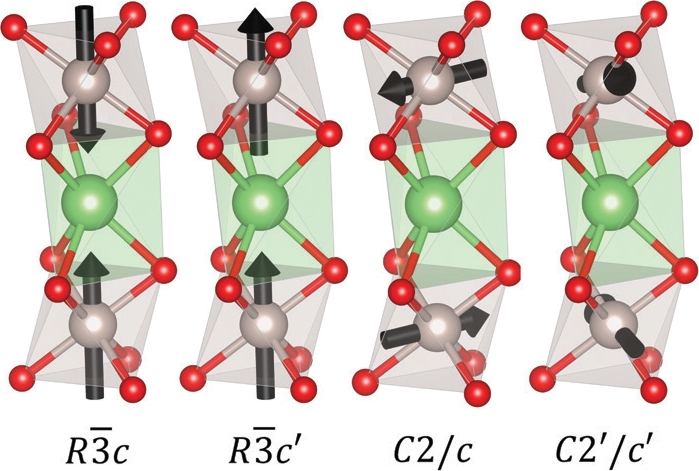
Distinguishing between some of these arrangement is trivial, e.g. R-3c and R-3c’ give rise to different peaks and would lead to different magnetic susceptibility, but the distinction becomes elusive moving from left to right along Fig. 2, in particular when we look at the two configurations labelled C2/c and C2’/c’. In these last cases the reduction from trigonal to monoclinic symmetry of the magnetic structures also allows the formation of three magnetic domains related by 120 degrees rotation about the c hexagonal axis.
High quality single crystals were measured at the Ru L3 (2.838 keV) absorption edge on the Materials and Magnetism beamline (I16) at Diamond Light Source. Besides the scientific problem, an element of interest associated with this study was to explore the possibility of extending the energy range of the I16 beamline well below the initially specified 3.4 keV. Dealing with low energy X-rays introduces many complications related to the very high absorption cross section, and in the case of I16 the limitation was mainly dictated by the initial specification of the monochromator. By performing four bounces on the channel-cut monochromator and adjusting all the existing optics accordingly to compensate for the new position of the X-ray beam, it was possible to get the beam in the experimental hutch. Care was taken to minimize the in-air path, reduce the absorption and push the ability of the area detector to its limit to detect low energy photon, even if with low efficiency.
A large resonant enhancement (Fig. 3) was observed below the Néel temperature at several glide plane forbidden reflections with an intensity close to 0.1% of the weakest charge reflections confirming the expected k=(0,0,0) propagation vector; no extra intensity appeared on top of the charge allowed reflection.
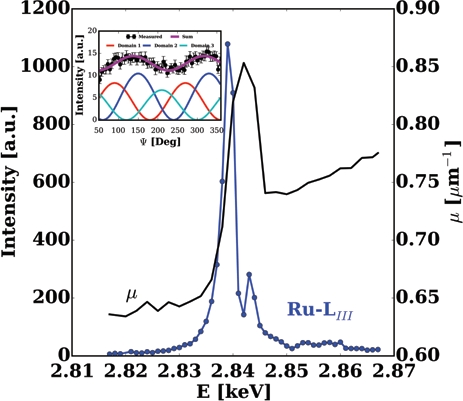
Figure 3: Resonant x-ray diffraction measured at the Ru L3 (2.83 keV) absorption edge at the magnetic (021) reflection in Sr3LiRuO6 at 8K. The absorption coefficient u was determined from fluorescence spectra measured at 300K. Inset: azimuthal dependence of the (0,0,3) reflection in the Li case measured at the maximum of the resonance. The fitting function, in purple, is the weighted sum of the monoclinic domains shown as red, blue and green curves.
Azimuthal scans (rotations of the crystals about a reflection maintained in diffraction condition) about the magnetic reflections indicate some differences in the two samples, with the Sr3LiRuO6 reflection flatter than the same reflection in Sr3NaRuO6, with the minima of this curve not reaching zero intensity. Simple simulations of the magnetic structure show that a flat azimuthal dependence would be the signature of a moment lying along the c axis, however, neutron measurements exclude this possibility. Another way to interpret such a result is to consider multiple magnetic domains contributing to the reflections as a result of the loss of the trigonal symmetry. Such an approach provides an excellent agreement with the data (inset of Fig. 3) and allows us to extract the domain fraction, which varies between the two samples. The distinction between the C2/c and C2’/c’ configurations remain elusive, however. It is only through a detailed analysis of the possible contributions to the free energy expansion (expanding the thermodynamic free-energy in terms of symmetric magnetic and atomic displacements) that it was possible to show that the in-plane spin configuration with the C2’/c’ magnetic symmetry is energetically favourable and can be physically understood considering the antisymmetric Dzyaloshinskii-Moriya (DM) exchange as the dominant anisotropic interaction in the system coupling the in plane AFM order with FM order along the c axis. This antisymmetric exchange is imposed by distortions induced through a magnetoelastic coupling involving ionic distortions too small to experimentally observe.
The combination of several experimental techniques as well as theoretical analysis was crucial in establishing the magnetic ground state of this family of compounds.
References:
Funding acknowledgement:
We acknowledge Diamond Light Source for time on Beamline I16 under Proposal No. 9409. We acknowledge ISIS Neutron Spallation Source for time on the instrument Wish under Proposal No. 1520273. Work at ISIS was supported by project TUMOCS. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant Agreement No. 645660. H.z.L. and A.C. acknowledge support from the NSF via Award No. DMR-1301757. C.M. thanks Diamond Light Source for their hospitality during this work. Images of atomic structures were created using the computer program VESTA, by K. Momma and F. Izumi.
Corresponding authos:
Dr Alessandro Bombardi, Diamond Light Source and University of Oxford, alessandro.bombardi (at) diamond.ac.uk, Dr Dan Porter, Diamond Light Source, dan.porter (at) diamond.ac.uk
Related publication:
Porter DG, Senn MS, Khalyavin DD, Cortese A, Waterfield-Price N, Radaelli PG, Manuel P, zur-Loye H-C, Mazzoli C, Bombardi A. Magnetostriction-driven ground-state stabilization in 2H perovskites. Physical Review B 94, 134404, doi:10.1103/ PhysRevB.94.134404 (2016).
Publication keywords:
4d-metals; 2H-perovskites; Magnetism
Diamond Light Source is the UK's national synchrotron science facility, located at the Harwell Science and Innovation Campus in Oxfordshire.
Copyright © 2022 Diamond Light Source
Diamond Light Source Ltd
Diamond House
Harwell Science & Innovation Campus
Didcot
Oxfordshire
OX11 0DE
Diamond Light Source® and the Diamond logo are registered trademarks of Diamond Light Source Ltd
Registered in England and Wales at Diamond House, Harwell Science and Innovation Campus, Didcot, Oxfordshire, OX11 0DE, United Kingdom. Company number: 4375679. VAT number: 287 461 957. Economic Operators Registration and Identification (EORI) number: GB287461957003.