Unconventional magnetic order in a 3D Kitaev material

The high-resolution, high-flux Materials and Magnetism beamline (I16) at Diamond Light Source was ideally suited for the study of the magnetism via resonant X-ray diffraction in small single crystals (less than 60 μm in diameter). The results of the experiments have been published in Physical Review Letters and have revealed a surprisingly complex magnetic structure. This cannot be understood based on conventional Heisenberg spin interactions alone, but require the presence of dominant Kitaev interactions to explain the complex features observed. This provides strong evidence that γ-Li₂IrO₃ is an experimental realisation of 3D Kitaev physics in the solid state. This provides strong evidence that γ-Li₂IrO₃ is an experimental realisation of 3D Kitaev physics in the solid state.

In the Kitaev model on the honeycomb lattice¹ the spins interact via nearest-neighbour Ising exchanges but where a different Ising axis (x,y,z) applies for the three different bonds emerging out of each lattice site. This leads to strong frustration effects that stabilise an exotic quantum spin liquid state. It was theoretically proposed² that such exotic Hamiltonians might be realised in magnetic materials containing edge-sharing cubic IrO₆ octahedra due to a combination of crystal field and spin-orbit coupling effects which stabilise complex spin-orbital J_eff =1/2 moments, which interact via Ising superexchange where the Ising axis is normal to the Ir-O₂-Ir plane². For a threefold coordinated IrO₆ octahedron, this leads to perpendicular Ising axes for the three nearestneighbor bonds, as required for a Kitaev model. In search of such physics the two-dimensional (2D) honeycomb-lattice α-Na₂IrO₃ and α-Li₂IrO₃ have been intensively explored, but as yet no clear evidence for novel Kitaev physics has been observed. The recent synthesis of a new structural polytype γ-Li₂IrO₃, which shares the same local three-fold coordination of edge-sharing IrO₆ octahedra but in a 3D lattice, opened up opportunities for potentially realising Kitaev physics in 3D. The purpose of the research reported here was to determine in detail the magnetic ground state and test for possible signatures of the presence of such exotic frustrated interactions. The availability of single crystals of only rather small sizes (under 60 μm diameter) as well as the high neutron absorption of Ir nuclei meant that neutron diffraction was not a viable route. However it turned out that the project was ideally suited for Magnetic Resonant X-ray Diffraction (MRXD) using the high-flux and high-resolution I16 beamline.

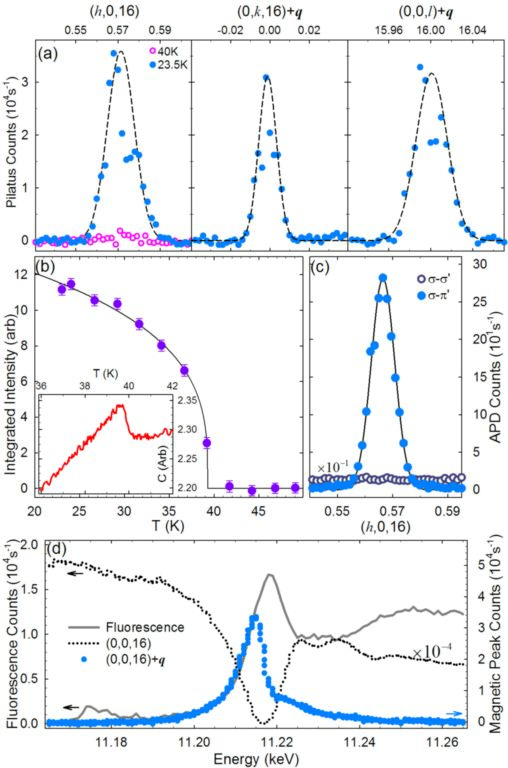Figure 1: Magnetic Bragg peak at (0,0,16)+q. (a) Scans along orthogonal directions in reciprocal space [filled (open)symbols at base temperature (above TN)]. Dashed lines are fits to a Gaussian shape. (b) Temperature dependence of the integrated magnetic peak intensity (solid line is guide to the eye). Inset: specific heat data. (c) Polarisation analysis:magnetic signal is present only in the σ-π' channel (filled circles) and disappears in the σ-σ' (open circles, intensity scaled by 1/10). (d) Energy scan through the magnetic peak(blue), a structural Bragg peak (dotted line, scaled by 1/104)as well as the fluorescence scan (solid line).

During the MRXD experiments systematic searches along high-symmetry directions in reciprocal space found that new magnetic Bragg peaks appeared at satellite positions of reciprocal lattice points with an incommensurate propagation vector q = (0.57(1),0,0) as illustrated in Fig. 1a. Those satellite peaks disappeared upon heating (Fig. 1a, open circles) via a typical order parameter temperature dependence (Fig. 1b), and have a large resonant enhancement in energy scans, as expected for magnetic scattering. The magnetic character was further confirmed via polarisation analysis: Fig. 1c shows that the peak at (0,0,16)+q appeared only in the rotated σ-π’ channel (filled circles) and is absent in the σ-σ’ channel (open circles), as expected for resonant diffraction that is of pure magnetic origin.

The observation of incommensurate magnetic Bragg peaks indicates a momentrotating or an amplitude-modulated structure with a periodicity that is incommensurate with the underlying crystal lattice. In order to distinguish between those two generic scenarios, and to determine the orientation of the magnetic moments at all magnetic sites in the unit cell, we analysed the magnetic structure in terms of symmetry-allowed basis vectors. The magnetic iridium ions are located on two inequivalent sublattices in the orthorhombic unit cell (light and dark balls in Fig. 3), each containing four sites in the primitive cell labelled 1 to 4 and 1’ to 4’, respectively. Four types of magnetic basis vectors exist for each of the two sublattices, denoted as ++++ (F), ++– (C), +–+ (A), and +–+– (G), where the ± signs denote the relations between the Fourier components at the four sites. Analysing the observed selection rules for magnetic scattering we identify that the ground state contains basis vectors F and A. We exploit the polarisation dependence of the MRXD intensity (probed via azimuthal scans) to deduce directly the polarisation of the magnetic moments and the relative phases between the components along different directions. Fig. 3 shows such azimuthal scans where the solid red line is a fit to the magnetic structure model with the relative moment magnitudes M_x:M_y:M_z = 0.65(4):0.58(1):1 and basis vectors in the combination i(A,−A)_x , i(–1)^m(F, −F)_y , (F,F)_z where m = 1 or 2 and the two labels in the brackets correspond to the two Ir sublattices. Other combinations of basis vectors can be clearly ruled out, as illustrated by the other lines (blue and green) in Fig. 2c. The magnetic structure corresponding to m = 1 is plotted in Fig. 3. The moments are confined to rotate in one of two planes, obtained from the (ac) plane by rotation around the c axis by an angle ±Ф, with Ф= tan^-1(M_y/M_x)=42(2)°. The pattern is such that neighbouring iridium zigzag chains have alternate orientations of the moment rotation plane as indicated by the light and dark shaded envelopes in Fig. 3. The m = 2 case simply gives the opposite alternation of the rotation planes.

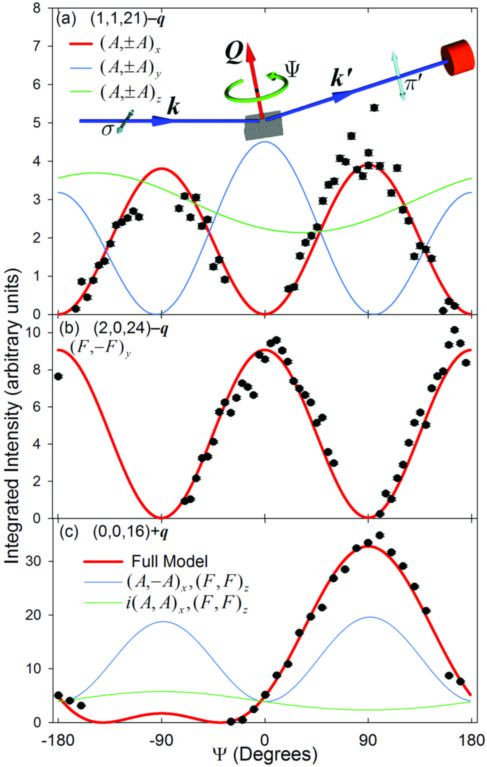
Figure 2: Integrated intensity as a function of azimuth for threemagnetic Bragg peaks (a) pure A_x, (b) pure F_y, and (c) mixed F_zA_x.Top diagram illustrates the scattering geometry. Data points (filledcircles) are integrated peak intensities from rocking curve scanscorrected for absorption and Lorentz factor. Thick (red) lines showfits that include all contributions to the MRXD structure factor fromthe magnetic structure model i(A,−A)_x, −i(F, −F)_y, (F,F)_z, depicted inFig. 3. Blue and green curves in (a) and (c) illustrate that other phasecombinations of basis vectors are ruled out.

A key feature of the magnetic structure is the counter-rotation of neighbouring moments. This pattern cannot be stabilised by Heisenberg interactions alone, but surprisingly the counter-rotation can be stabilised by Kitaev interactions. This can be intuitively seen by inspecting the 3^rd unit cell of Fig. 3. Note that along the zig-zag chain for all the x-bonds (black) spins are on average parallel when oriented along x (to gain energy from the Kitaev ferromagnetic interaction along x) and antiparallel when oriented along y (to gain energy from the antiferromagnetic Heisenberg exchange), and similarly for the bonds of the opposite type (y). The noncoplanarity (2^nd unit cell Fig. 3) allows for an equivalent stabilisation across a z (red) type bond.

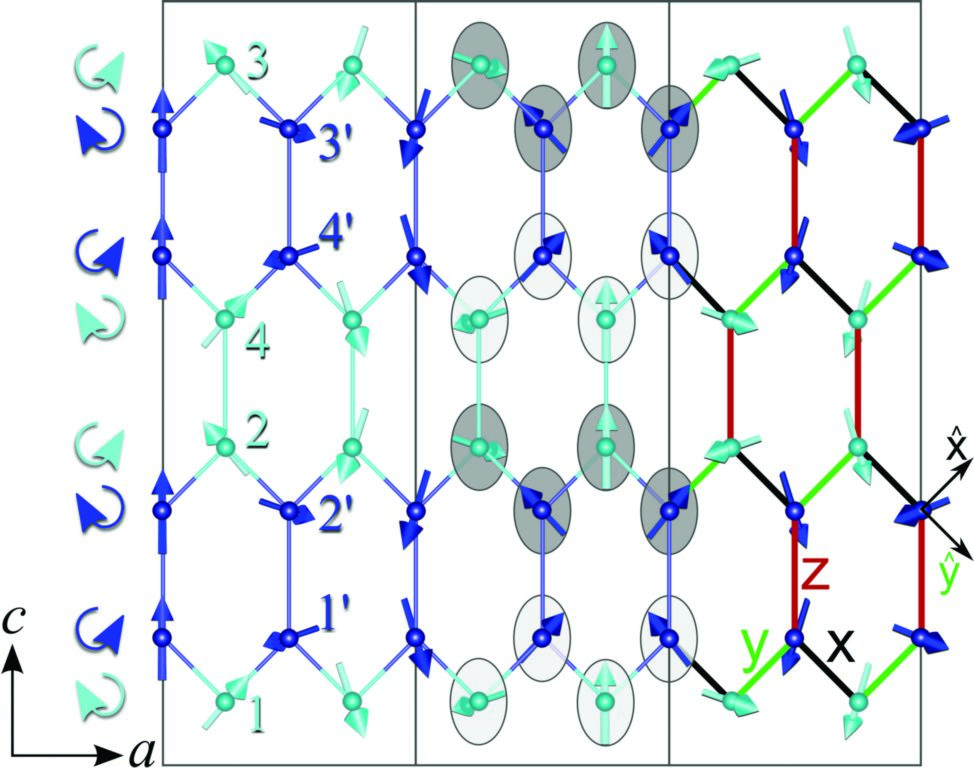
Figure 3: Magnetic structure projected on the (ac) plane showing three unit cells along a. Light/dark blue arrows show the moments on the Ir/Ir’ sublattices, with sites 1–4 and 1’–4’, respectively. Curly arrows illustrate counter-rotating magnetic order between consecutive sites along c. In unit cell 2, light (−Ф) and dark (+Ф) shaded elliptical envelopes emphasise the confinement of moments to alternate planes, rotated by ±Ф around c. In unit cell 3, the colour of bonds (black/green/red) indicates the anisotropy axis, x,y,z, of the Kitaev exchanges, where the directions of x and y are indicated and z points into the page.

To summarise, through MRXD measurements on γ-Li₂IrO₃ single crystals, an incommensurate, noncoplanar magnetic structure with counter-rotating moments has been observed. A Kitaev-Heisenberg Hamiltonian can explain all features of the observed complex magnetic structure, providing strong evidence that γ-Li₂IrO₃ is an experimental realisation of 3D Kitaev physics in the solid state.

Source publication:
Biffin, A., Johnson, R. D., Kimchi, I., Morris, R., Bombardi, A., Analytis, J. G., Vishwanath, A. & Coldea, R. Noncoplanar and Counterrotating Incommensurate Magnetic Order Stabilized by Kitaev Interactions in gamma-Li2IrO3. Physical Review Letters 113, doi:10.1103/PhysRevLett.113.197201 (2014).

References:
1. Kitaev, A. Anyons in an exactly solved model and beyond. Annals of Physics 321, 2-111, doi:10.1016/j.aop.2005.10.005 (2006).

2. Chaloupka, J., Jackeli, G. & Khaliullin, G. Kitaev-Heisenberg Model on a Honeycomb Lattice: Possible Exotic Phases in Iridium Oxides A(2)IrO(3). Physical Review Letters 105, doi:10.1103/PhysRevLett.105.027204 (2010).

3. Kim, B. J. et al. Phase-Sensitive Observation of a Spin-Orbital Mott State in Sr2IrO4. Science 323, 1329-1332, doi:10.1126/science.1167106 (2009).

4. K. A. Modic, T. E. Smidt, I. Kimchi, N. P. Breznay, A. Biffin, S. Choi, R. D. Johnson, R. Coldea, P. Watkins-Curry, G. T. McCandless, J. Y. Chan, F. Gandara, Z. Islam, A. Vishwanath, A. Shekhter, R. D. McDonald, and J. G. Analytis, Realisation of a three-dimensional spin–anisotropic harmonic honeycomb iridate. Nat. Commun. 5, 4203 (2014).

Funding acknowledgements:
This work was supported by EPSRC (UK) under Grants No. EP/H014934/1 and No. EP/J003557/1, and by the US Department of Energy, Office of Basic Energy Sciences, Materials Sciences and Engineering Division, under Contract No. DE-AC02-05CH11231.

Corresponding authors:
Dr Alun Biffin, Paul Scherrer Institut, [email protected]; Dr Roger D. Johnson, University of Oxford, [email protected]; and Radu Coldea, University of Oxford, [email protected]