Counting topological knots by X-rays

Symmetry breaking is one of the core concepts of condensed matter physics. To understand a system, the most important question to ask is: what is its underlying symmetry? Symmetry underpins the properties of a material both on a microscopic and macroscopic scale, and it captures the fundamental physics needed to describe a system. This theoretical approach has been very successfully applied to the description of experimental systems in the recent past. For example, diffraction experiments and microscopy techniques were developed to determine the crystal symmetries of a material. Once the symmetry is unambiguously determined, almost all its physical properties can be inferred or calculated.

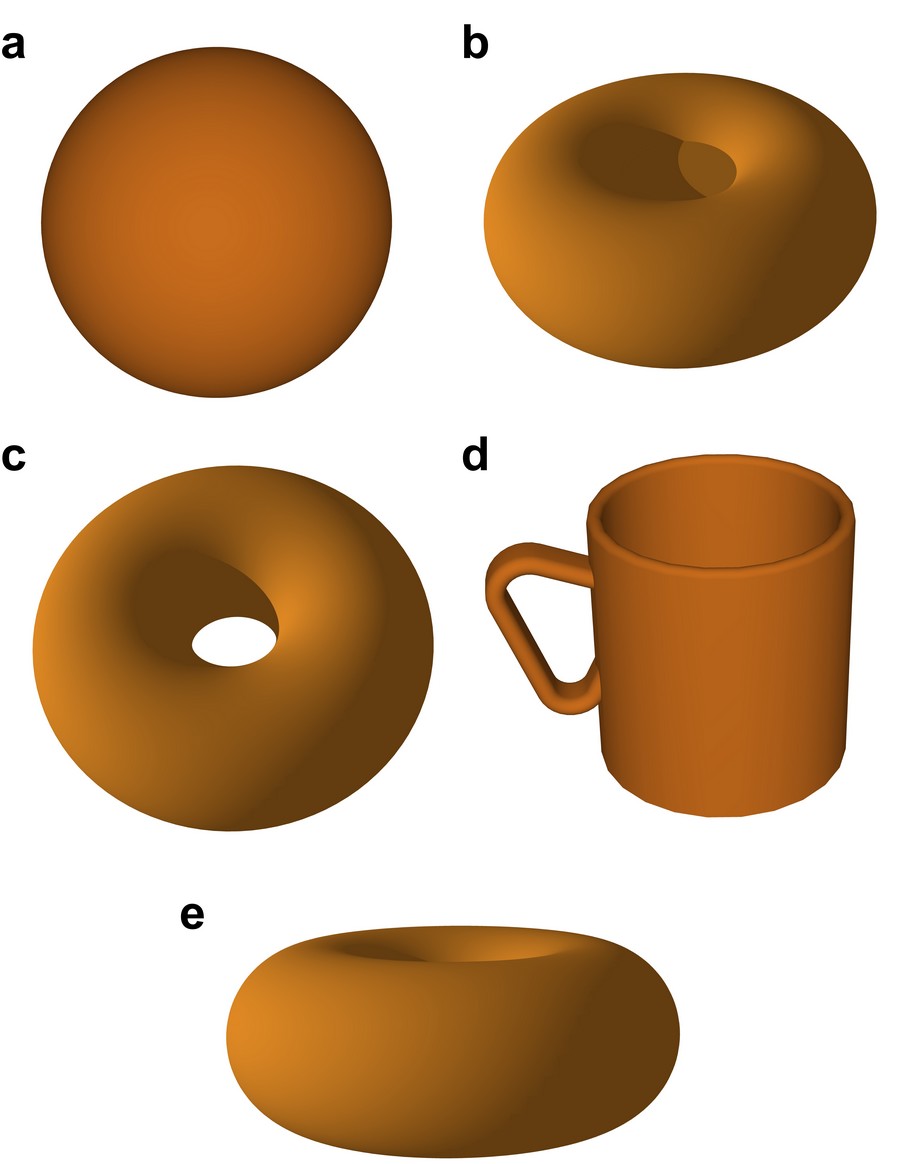
Figure 1: Topological objects commonly found at every police stake out across North America, coffee mugs and doughnuts. (a,b) Sphere, (d) coffee mug, and (c,e) a doughnut seen from different perspectives.

In order to gain an even deeper understanding of a system, another useful question to ask is: what is the underlying topology? Unlike symmetry, the mathematical concept of topology describes the geometrical properties and spatial relations unaffected by a continuous change of shape or size of an object. In the example shown in Fig. 1, the pristine (a) and the squeezed ball (b) have completely different symmetries, yet a continuous deformation can transform one into the other. Therefore, they are said to be topologically equivalent. On the other hand, it is not possible to transform them into a doughnut, or a cup, by performing continuous deformation, unless a “hole” is punched through the object. Therefore, a ball has a distinctly different topology from a donut. In fact, an invariant, called genus number, can be introduced to define the topological property. This number essentially counts the number of holes of an object and describes how well a topological state is ‘protected’ from being transformed into another state with different genus number.

The next question is: how can one experimentally measure such a topological property? Take the example of the genus number: the most primitive way is to simply look at the object. If a complete and detailed three-dimensional image of the object can be determined, the topological information should come for free. However, as it turns out, direct imaging may very often lead to the wrong conclusion. Take for instance the ball in Fig. 1(a,b), which has a genus number of zero. Once a hole is punched into it (c), this number becomes one, however, if the hole is small or the perspective is unfavourable (e), an image of the object with its inherent limitations can easily lack the crucial details. Therefore, real-space imaging method is a rather indirect way of determining the topological property. In other words, the proper way of identifying the genus number is to go via its mathematical definition.

This topological concept can be applied to the field of magnetism where it is used to classify magnetic order. Apart from the topologically trivial magnetic orders, e.g. ferromagnetic or antiferromagnetic order, non-trivial magnetic states have been recently identified as well, so-called magnetic skyrmions. These magnetization swirls have the spin pointing up in the core of the vortex, and down in the surrounding boundary. The entire vortex-like configuration possesses a non-trivial topology, which prevents it from unwinding back to a trivial, uniformly aligned magnetic state with ease. Therefore, skyrmions are a ‘topologically protected’ magnetic state, which is a promising candidate for future information carriers. Moreover, such unique magnetic structures open up the door to novel physics, e.g. emergent electromagnetics, which could lead to promising spintronics applications.

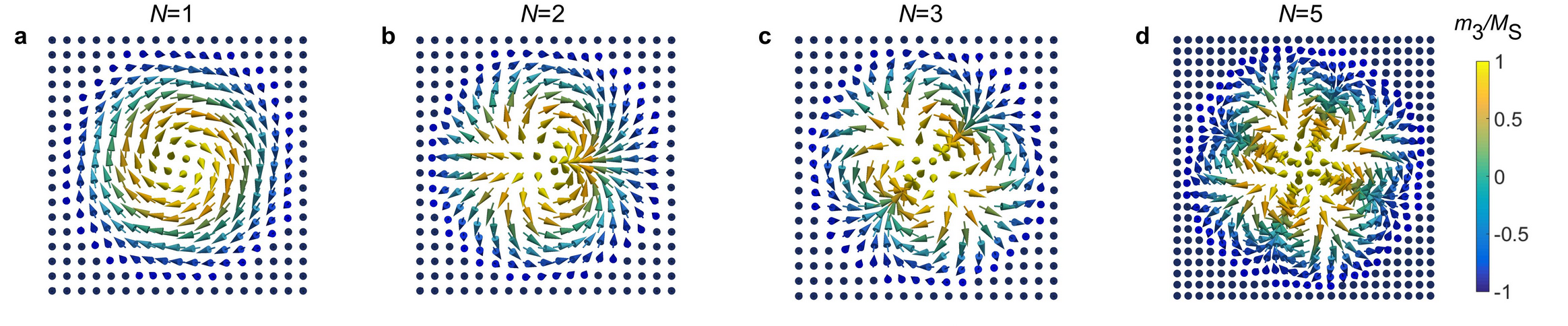
Similar to the genus number, an integer number N, called winding number, can be defined to classify the topological properties of these spin textures. It is essentially the total number of times that a curve travels around a point. Illustrations of N = 1, 2, 3, and 5 skyrmions are shown in Fig. 2. But how can one measure the winding number of a topologically ordered state? Perhaps the most successful experimental techniques that allow for their measurement are magnetic microscopy methods. For example, in Lorentz transmission electron microscopy, a ‘snapshot’ of the magnetisation pattern is taken. By comparing the magnetic contrast image with a theoretical model, the winding number can be inferred. However, analogous to the practical issue of determining the genus number, the microscopy image only provides a certain perspective – not the topological information. Consequently, magnetic imaging is not always a reliable tool for the determination of the winding number.

Recently, a team of scientists from the University of Oxford and Diamond Light Source carried out a study demonstrated that the topological winding number – the single most important property of a topological spin system – is directly accessible through the light-matter interaction. It is naturally encoded in the polarisation dependence of the resonant X-ray scattering process, which is a universal process applicable to many different materials and systems. The scientists introduced the topology determination principle and presented analytical solutions, numerical calculations, as well as experimental data, which are all in excellent agreement. Most importantly, they demonstrated that this novel technique is exclusively sensitive to the winding number, which allows for the accurate and unambiguous determination of a spin system’s topological key quantity. Experiments proving the validity of this new principle were carried out on Diamond’s BLADE: X-ray Dichroism and Scattering beamline (I10). The RASOR diffractometer with its ultrahigh resolution is ideally suited for characterizing the topologically non-trivial skyrmion state such as in the magnetoelectric material Cu₂OSeO₃.

“It is crucial that a systematic methodology can be developed that is able to measure the topological properties of a state, very much like crystallographic experiments were developed to study the symmetries of a system”, said Dr Shilei Zhang, the lead scientist from Oxford. “Thanks to RASOR, we are now able to experimentally realise this method, which is elegantly associates the mathematics of topology with experimentally determinable quantities. We are looking forward to discovering more applications of this principle.”

To find out more about the I10 beamline, or to discuss potential applications for, please contact Principal Beamline Scientist Dr Paul Steadman: paul.steadman@diamond.ac.uk.