The development of high temperature superconductors would allow the conservation of huge amounts of energy lost to electrical resistance during transmission to consumers, as well as the development of new technologies such as high performance electrical motors, superconducting magnets for MRI scanners and magnetic levitation trains. However, the mechanism behind high-temperature superconductivity is not yet understood.
A team of researchers used Diamond Light Source’s Angle resolved photoemission (ARPES) beamline (I05) to investigate the electronic structure of iron-based superconductors. ARPES is the most direct probe of electronic band dispersion, and is ideal for mapping the dispersion of electronic bands near the Fermi level - the highest occupied energy level of the material.
The researchers were looking at spin-orbit coupling; a fundamental interaction that can promote and stabilise superconductivity, allow ferromagnetism to coexist with superconductivity, and even raise the temperature at which superconductivity occurs.
The results showed fine splitting of the electronic states close to the Fermi level. Comparison with band-structure calculations showed this splitting to be a result of spin-orbit coupling, although prior to these experiments the effects of spin-orbit coupling in iron-based superconductors was considered insignificant. These new findings are therefore likely to make an important contribution to new theories that help us to explain, and then harness, high-temperature superconductivity.
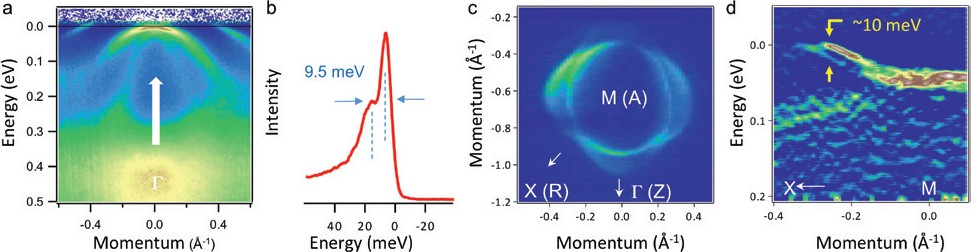
Figure 1: (a) ARPES data along the high-symmetry direction in LiFeAs multiplied by the Fermi function. (b) Energy-distribution curve corresponding to zero momentum in panel (a). (c) High-precision Fermi surface map of electron pockets in LiFeAs. (d) Second derivative of ARPES intensity recorded along the MX-direction.
Spin-orbit coupling (SOC) is a fundamental interaction between the spin of the particle and its orbital motion. In its presence, the spin of electron quantised along any axis is no longer a good quantum number and the electronic states are better described by the total angular momentum. This interplay may split the electronic states and lead to the fascinating physical phenomena such as spin Hall effects, spin relaxation, topological insulation, occurrence of Dirac, Majorana and Weyl fermions, etc. It is therefore no wonder that the systems with SOC are the focus of intensive research in the field of spintronics. There is a unique opportunity to manipulate the spin without the aid of magnetic field.
A special role has been played by SOC in superconductivity. It can promote and stabilise superconductivity1, allow ferromagnetism to coexist with superconductivity2, or even raise the transition temperatre (Tc) 3. SOC could be a very important ingredient in describing the superconducting state in those materials, where it is comparable to, or larger than, the superconducting gap. In iron-based superconductors (IBS), where the low-energy electronic states are composed of different orbitals, SOC-induced spin anisotropy, together with the orbital mixing, may directly influence the orbital and spin angular momentum of the Cooper pairs, thus making the determination of the pairing symmetry non-trivial. However, until now SOC in IBS was considered insignificant.
In order to detect the SOC in IBS we have studied many materials at beamline I05. Among them is LiFeAs - a special representative of iron-based family of superconductors4. This material is one of the most studied due to its stoichiometry and non-polar surfaces and its electronic structure is believed to be well understood from numerous ARPES experiments. According to the band structure calculations, the most convenient places to detect the spin-orbit splitting in LiFeAs is exactly in the center of the Brillouin Zone (BZ) and at the BZ-boundary where it crosses the electron-like pockets. In Fig.1a we show the ARPES data taken along the high-symmetry direction in the BZ running through the G-point. From this intensity plot one is able to resolve three hole-like dispersions forming the corresponding Fermi surface pockets around G. Two of the dispersions have their maxima below the Fermi level and these are non-degenerate, i.e. the tops of these bands are located at slightly different binding energies. This is confirmed by Fig.1b where the energy-distribution curve taken at zero momentum is shown. There are two features separated by 9.5 meV and this distance is due to SOC.
To measure the magnitude of the SOC on the electron pockets we had to switch to another location in the k-space. Since the SOC split dispersions cross the Fermi level in (kx, ky) plane, we can observe this splitting in the momentum space with high resolution. We have recorded the detailed Fermi surface map near the corner of the BZ especially for this purpose. Indeed, as follows from Fig.1c, electron pockets are no longer degenerate along the MX-direction, contrary to what is expected from non-relativistic band structure. To quantify the effect in terms of energy, we plot the intensity as a function of momentum along MX and energy in Fig.1d. The dispersions are again split by ~10 meV demonstrating the lifting of the degeneracy of electron pockets along the high symmetry directions and closely corresponding to the value determined in the centre of the BZ. As predicted by the calculations, we have thus directly observed the SOC in LiFeAs.
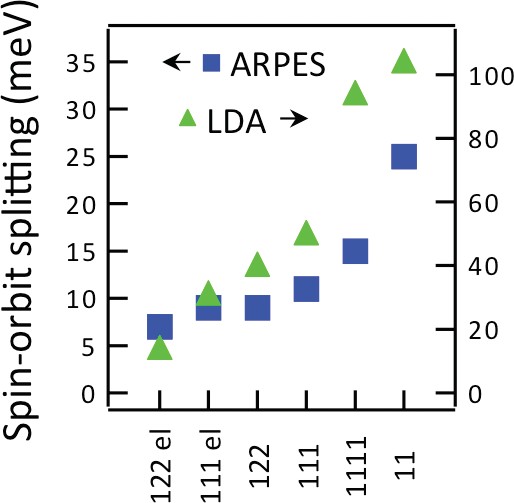
Similar experiments on FeSe have revealed the presence of SOC and supported the dominant role of this interaction in comparison with the nematic splitting5. The analogous data for other two main families of IBS, 122 and 1111, have also featured the characteristic splitting of the states in the center of the BZ and on electron pockets. We summarise our observations in Fig. 3 where we plotted the experimentally determined values of SOC together with those predicted by the band structure calculations. There is a clear correlation between the two datasets, which speaks in favor of our interpretation of the observed splitting. We note that experimental value for FeSe is slightly overestimated since the nematic order contributes to the splitting at the center of the BZ, but this contribution remains noticeably smaller than that of SOC.
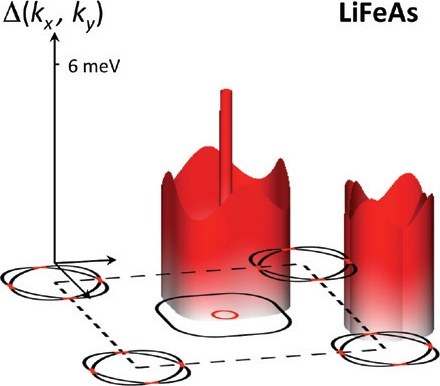
We expect that these findings are highly relevant for superconductivity in IBS. In Fig. 3 we schematically show the Fermi surface contour and gap function for LiFeAs. We mark in red those Fermi surfaces or their portions which are formed by the spin–orbit split states. Remarkably, the largest superconducting gap is supported by the SOC-induced Fermi surfaces. We have confirmed such behaviour for the main representatives of the IBS superconductors: 11, 122 and 111.
We have thus observed the decisive influence of the spin–orbit interaction on the low-energy electron dynamics of all representative iron-based superconductors. The size of SOC is comparable to the pairing gap and the Fermi energy, which may have profound implications on the mechanism of superconductivity in these materials.
References:
Funding acknowledgement:
We acknowledge Diamond Light Source for access to beamline I05 (proposals no. SI10372 and SI11643). The work was supported under grants No. BO1912/2-2, BO1912/3-1, BE1749/13 and WU595/3-1.
Corresponding author:
Dr Sergey Borisenko, IFW-Dresden, [email protected]
Related publication:
Borisenko SV, Evtushinsky DV, Liu Z-H, Morozov I, Kappenberger R, Wurmehl S, Büchner B, Yaresko AN, Kim TK, Hoesch M, Wolf T, Zhigadlo ND. Direct observation of spin-orbit coupling in iron-based superconductors. Nature Physics 12, 311–317 doi:10.1038/nphys3594 (2016).
Publication keywords:
Superconductivity; Spin-orbit interaction; Angle-Resolved Photoemission Spectroscopy (ARPES); Iron-based superconductors
Diamond Light Source is the UK's national synchrotron science facility, located at the Harwell Science and Innovation Campus in Oxfordshire.
Copyright © 2022 Diamond Light Source
Diamond Light Source Ltd
Diamond House
Harwell Science & Innovation Campus
Didcot
Oxfordshire
OX11 0DE
Diamond Light Source® and the Diamond logo are registered trademarks of Diamond Light Source Ltd
Registered in England and Wales at Diamond House, Harwell Science and Innovation Campus, Didcot, Oxfordshire, OX11 0DE, United Kingdom. Company number: 4375679. VAT number: 287 461 957. Economic Operators Registration and Identification (EORI) number: GB287461957003.